Recall we previously introduced the notion of "object oriented mathematics" by defining a "Mathematical Object", then insisted that every definition in mathematics defines a mathematical object (in the sense that everything defined in math is-a mathematical object). We then proceeded to introduce a lot of category theoretic concepts, like morphisms as generalized structure-preserving maps from one object to another, categories as a sort of directed network whose nodes are mathematical objects and whose edges are morphisms, functors as a morphism of categories, natural transformations as morphisms of functors, and so forth. Now wouldn't it be lovely if this all tied together "somehow"?
The recommended reading this time is a little light, since I don't really know of any good references on this material (perhaps some needs to be written!). Therefore I am going to include material on "stuff, structure, and properties":
- John Baez "Quantum Quandaries: A Category Theoretic Perspective", arXiv:quant-ph/0404040
- John Baez and Derek Wise "Quantization and Categoriefication: Properties, Structures, 'n' Stuff!" Lecture Notes, 2004.
- John Baez and Michael Shulman "Lectures on n-Categories and Cohomology", arXiv:math/0608420
- John Baez and J Dolan "From Finite Sets to Feynman Diagrams", arXiv:math/0004133
- John Baez et al. Discussion Spring Quarter (2004)
- Jeffrey Morton, Categorification and Matter Theoretical Atlas (2008)
- The entry in nLab wiki
- John Baez Universal Algebra and Diagrammatic Reasoning Lectures at Geometry of Computation (2006)
- Steve Awodey Lecture Notes on Categorical Logic parts I, II, and III.
The Basic Algorithm
What we are going to do is pretty algorithmic. We are going to show all our work deriving this algorithm, so lets start by guessing at what it could be. The "obvious" approach (at least to me) is to use the following dictionary:
| Category Theory | Our "Object Oriented" Scheme |
| Objects of a Category | Stuff |
| Morphisms | Structure |
| Commutative Diagrams | Properties |
This "seems" like a good idea, so lets try it out on groups and see what we need to "forget" a group "into" a monoid.
Example: A Group
We are going to test our algorithm now by setting up a category to describe the notion of a group, and we are going to see how it behaves when we "forget" the inversion operator.
So we basically have our stuff be represented by the set of objects $\{G^{k}|k\in\mathbb{N}\}$ where $G^{0}$ = 1, and $G^{k}=G\times(\cdots)\times{G}$ ($k$ times). For our purposes with a group, we only need $k=0,1,2,3$, anything else is overkill.
Our structure consists of: the multiplication operator $m:G\times{G}\to{G}$; the identity element $e:\mathbf{1}\to{G}$; and the inversion operator $i:G\to{G}$.
The properties we want our group to satisfy are associativity of multiplication, which is equivalent to demanding the following diagram commutes:
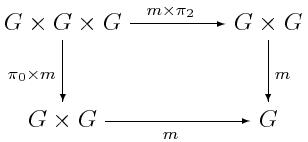 and various properties of the identity and the inverse summarized by the demand the following diagrams commute (respectively):
and various properties of the identity and the inverse summarized by the demand the following diagrams commute (respectively):

We should probably see how to "demote" our category theoretic description of a group, from a category to a mere object in Grp. To do so first consider what a group homomorphism amounts to. It maps the identity to the identity, and preserves multiplication. This sounds a lot like a functor.
If we just insist that $F$ (our group homomorphism) maps $G$ to $F(G)=H$ some other group, and $e$ to $F(e):\mathbf{1}\to{H}$, $m$ to $F(m):H\times{H}\to{H}$, and maps inverses to inverses so $i$ to $F(i):H\to{H}$, then all the properties of the group are preserved since functors preserve composition of morphisms (and thus they preserve commutative diagrams!).
So in a sense, what we are doing is "promoting" the objects of Grp to categories, then - for consistency - the morphisms are "promoted" to functors. To summarize the relation between the "instance" of a group we've constructed and the category of groups, consider the following table:
| Grp | Instance |
| Object | Category |
| Morphisms | Functors |
| Functors | Functors Again? |
What would the "forgetful functor" $U:$ Grp→Set look like in this scheme? Well, it would be a sort of "2-functor" that would be, one assumes, "2-faithful".
Forgetting A Group "Into" A Monoid
We want to "forget" the group into a monoid, what do we mean by this? Well a group "is-a" monoid equipped with an inversion operator such that a diagram commutes. We want to forget the inversion structure and consequently the properties it satisfies.
The "stupid simple" answer is fairly obvious: the "2-functor" from our "2-Grp" to "2-Mon" would be an embedding. Why? Because the inversion operator is just a homomorphism which maps $x$ to $x^{-1}$, and $e$ to $e^{-1}=e$. This requires "promoting" the inversion morphism to be an inversion functor, which is an illegal maneuver. So this "stupid simple" way to "forget" a group into a monoid can't work.
Perhaps we should just map the inversion operator to the identity morphism on $G$, that is $1_{G}$? This means that it is no longer faithful it's instead full...but it has the added bonus that it works.
It seems that this approach to describing "stuff, structure, and properties" was not in mind when Baez wrote:
There are various amounts of forgetfulness that [a functor] p can have:
- p forgets nothing if it is an equivalence of categories, i.e. faithful, full, and essentially surjective. For example the identity functor Ab→Ab forgets nothing.
- p forgets at most properties if it is faithful and full. E.g. Ab→Grp, which forgets the property of being abelian, but a homomorphism of abelian groups is just a homomorphism between groups that happen to be abelian.
- p forgets at most structure if it is faithful. E.g. the forgetful functor from groups to sets, Ab→Set, forgets the structure of being an abelian group, but it’s still faithful.
- p forgets at most stuff if it is arbitrary. E.g. Set2→Set, where we just throw out the second set, is not even faithful.
arXiv:math/0608420.
(Author's Note: I have modified the quote so it uses the conventions of this blog (e.g. Sets became Set, etc.) and - as usual - the category names have been made into links.)
So our current endeavor would require:
- a way to translate our category theory description of a particular mathematical object into an object of a corresponding category (denoted for brevity as Obj);
- a way to translate an object of Obj into our category theory description of the particular mathematical object.
So to describe our predicament using diagrams (as category theorists love doing), we basically are demanding the following commutes:
![\begin{diagram}[heads=LaTeX]
\mathbf{Obj} & \rTo^{U} & \mathbf{Ob}\\
\uInto & & \dTo\\
\mathbf{O} & \rDashto_{forget!} & \mathbf{N}
\end{diagram}](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj_50kbHiT2uzNwHGe1a1cI8e-UCU4Rx4AvEyRvDUUZJL2vOpXt5Hj48ptrqmFCTHTJrDmchio3zhL6iTuV3GoicOgfKCwdQsfzjEALImsbdU_lPsaQZARZCLKa4AGXmLx-yigB7OiBgYg/s400/moreObjectOrientednessImg3.png) We embed the object of interest O into the category of corresponding objects Obj. We then "forget" something U:Obj→Ob (the category of slightly forgotten objects conveniently lacks the "j"). Then we recover the object as a category N, then assert there has to be a functor forget! which makes the diagram commute.
We embed the object of interest O into the category of corresponding objects Obj. We then "forget" something U:Obj→Ob (the category of slightly forgotten objects conveniently lacks the "j"). Then we recover the object as a category N, then assert there has to be a functor forget! which makes the diagram commute.
We see, however, that each morphism here is a functor, so our ability to forget a group G "into" a monoid should use a functor...but we should ultimately want to take a functor to a morphism, according to our table. It seems there is no way to construct such a functor forget! as we desire with the tools available at our disposal. We will have to revisit the issue of forgetfulness later on.
A 2-Category Description of A 1-Category Problem
I have been thinking about this problem we have, and the solution I think is this: we are using the language of 2-categories to describe a 1-category problem. It gives us extra information about groups, but it makes the problem a bit extra hard since the intuition we want to use doesn't apply here. First a reference...
- John Baez, This Weeks Finds, Week 83: Tales of n-Categories
Specifically Dr Baez writes:
What's a monoidal category, exactly? Roughly it's a category with some
sort of "tensor product" and "unit object". But we can precisely define
the so-called "strict" monoidal categories as follows: they are simply
2-categories with one object. (Turn to "week80" for a definition of
2-categories.) A 2-category has objects, morphisms, and 2-morphisms,
but if there is only one object, we can do the following relabelling
trick:
2-morphisms ---------> morphisms
morphisms ---------> objects
object --------->
Namely, we can forget about the object, call the morphisms "objects",
and call the 2-morphisms "morphisms". But since all the new "objects"
were really morphisms from the original single object to itself, they
can all be composed, or "tensored". That's why we get a category with
"tensor product", and similarly, a "unit object".
So, just as a category with one object is just a monoid, a 2-category
with one object is a monoidal category! This is one instance of a trick
that I sketched many more cases of in "week74".
This Weeks Finds.
This gives me hope that we didn't screw up too badly! We're just ahead of the curve! Unfortunately, I'll need to cover a bit more category theory before I can make any more meaningful progress in this direction. I'm just afraid that I might have accidentally wandered into the wilderness of 3-categories... After reviewing a bit more about category theory, I believe now that I have wandered into the wilderness of topos!
No comments:
Post a Comment